资讯内容
使用Scratch证明:周长一定时正多边形面积最大
吴俊杰老师于17年7月初发布了一道Scratch题目,如图所示。经过4个小时的奋战,我终于搞定了这道题目。下面我对本程序进行汇整、说明:首先介绍数学反证法证明周长一定时正多边形面积最大;接着介绍Scratch反证法的思路;然后介绍程序的操作方法;最后介绍程序的数学原理以及设计思路。
一、数学证明
首先证明等周定理,然后利用等周定理即可得到推论:等周多边形面积最大是其正多边形。等周定理的定义:在周长一定的所有封闭平面曲线中,圆所围的面积最大。下面先来证明等周定理。证明:设K是周长一定而面积最大的图形,只要证明K是一个圆即可。以下分三步来完成。
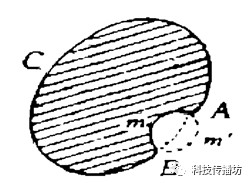
第一步:用反证法证明K是凸多边形。如下图所示,若K是一个凹图形, 那就一定可以在它上面找到两点A、B,其连线落在图形K的外部。以AB为轴,把曲线AmB对称到另一侧,称为曲线Am’M。图形AmBC与图形A m’BC的周长相等,而后者面积更大,这与K有最大面积矛盾。故K只能是凸图形。
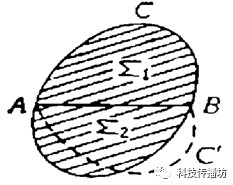
第二步:用反证法证明平分K的周长的弦也一定平分其面积。如下图所示,设凸图形K有最大面积,AB平分它的周长,且弦AB把K分成两部分Σ1和Σ2。Σ1≠Σ2,不妨设Σ1>Σ2,以AB为轴,把ACB对称到另一侧AC’B处,则周长ACBC’A等于K的周长,但面积ACBC’A>K的面积,这与K有最大面积矛盾。所以,平分K的周长的弦也一定平分其面积。
第三步:证明平分周长、面积的弦是直径,从而K为圆。 用反证法。设AB平分K的周长和面积,在K的边界上任取一点C,只需证ACB为半圆。若不然,∠ACB≠90°,将下图左侧中的Σ1、Σ2剪下来,贴成另一个图形(下图右侧),其中A’C’=AC,B’C’=BC,∠A’C’B’= 90°。这两个图形中,曲线ACB的长等于曲线A’C’B’的长,但后者面积较大,与K有最大面积矛盾。故ACB为半圆,从而K是圆。
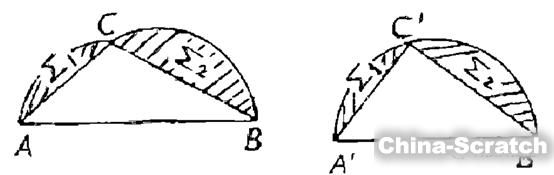
于是,证得了等周定理:在所有等周的平面封闭图形中,以圆的面积为最大。下面证明周长相等的多边形中,正多边形的面积最大。
证明:在所有周长相等的图形中,正多边形与圆形最接近,由等周定理的定义可知,正多边形的面积最大。
参考文献
《探索等周定理的推广及其应用》
https://wenku.baidu.com/view/277a9c6169eae009581bec99.html
二、Scratch反证法
根据之前的证明可知正多边形面积最大,因此本程序可能的设计思想如下:
-
展示如上数学证明思路。这样做虽然简单,但是很抽象,需要用户详细地跟随程序的指引完成证明过程。
-
给定正多边形,让用户拖拽多边形顶点,同时保证等周的条件。如果用户找不到更大面积的情形,即反证了本题目。这样做虽然复杂,但是用户体验好,且有数学证明保证正确性。本程序选择此设计方法。
三、程序操作说明
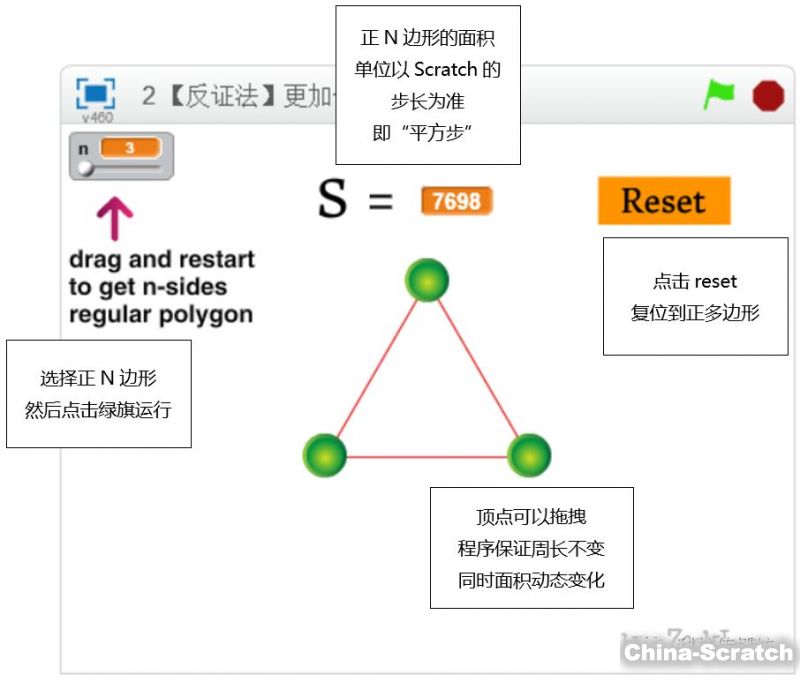
四、程序数学原理
本程序的难点在于拖拽顶点时保证等周,即周长不变。显然,椭圆的第一定义可以满足这一点:平面内与两定点F1、F2的距离的和等于常数2a (2a>|F1F2|) 的动点P的轨迹叫做椭圆。即 |PF1|+|PF2|=2a。
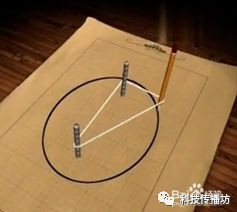
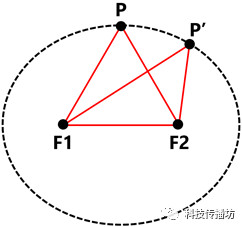
根据定义可知,F1P+F2P=F1P’+F2P’,这就是等周的关键。当点击某个顶点时,得到左右相邻两顶点的坐标,以此作为椭圆的两焦点,计算F1P+F2P后即可得到椭圆的各个参数,然后限制顶点P的移动再次椭圆轨迹上即可保证等周。椭圆的一般化参数方程如下:
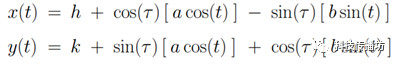
其中参数t决定了顶点位于椭圆线上的位置,可以设置为鼠标在舞台上的角度;参数τ是椭圆和x轴的夹角;参数a、b是椭圆的长短轴长度;(h, k) 是椭圆中心点所在坐标。
参考文献
《Using the Ellipse to Fit and Enclose Data Points》
http://www.cs.cornell.edu/cv/OtherPdf/Ellipse.pdf
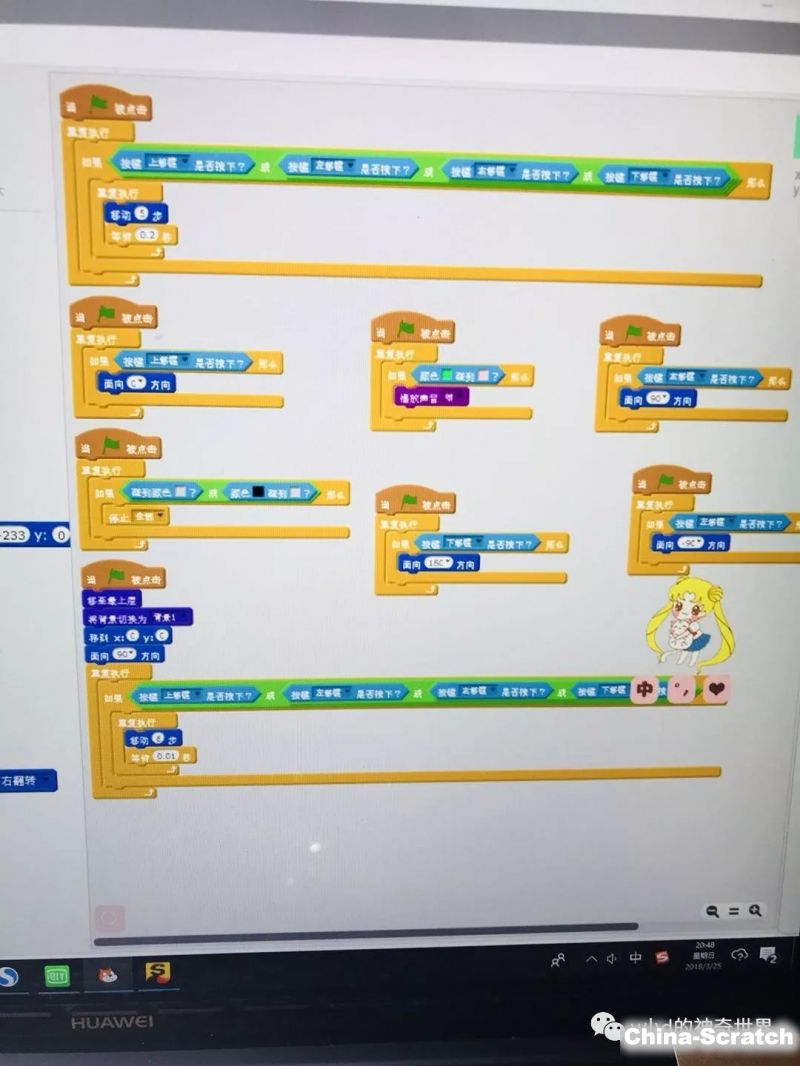
五、程序细节展示
本文仅展示核心脚本。当点击某个顶点后,程序会寻找该点左右相邻的两个顶点坐标:
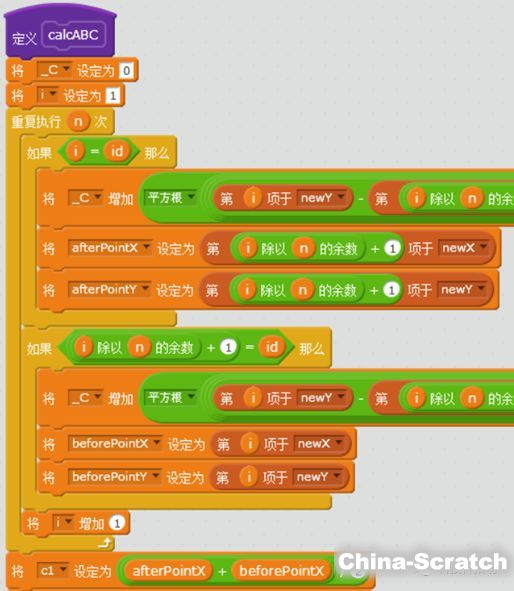
变量beforePointX和beforePointY是第一个相邻点(即椭圆的第一个焦点)的XY坐标,变量afterPointX和afterPointY是另一个相邻点(即椭圆的第二个焦点)的XY坐标。变量_C保存了当前顶点到两焦点的长度和,即椭圆第一定义中的2a。接着计算椭圆参数方程中的关键参数:
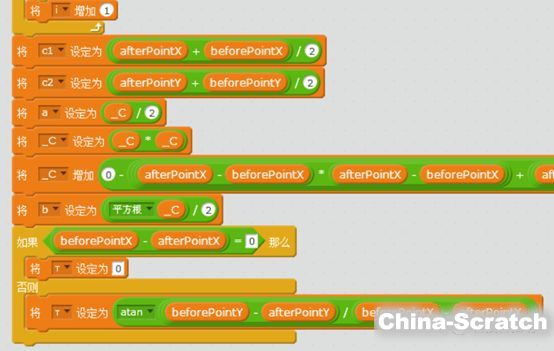
变量c1c2显然是椭圆中心点位置,即参数方程中的 (h, k);_C除以2即椭圆的半长轴a;根据椭圆a²-b²=c²可以计算变量b的值;最后计算τ,需要注意水平情况,即在椭圆未发生倾斜时,斜率公式分母为0,所以要特殊处理。得到基础数据后便可设置顶点的位置:

变量鼠标方向就是参数方程中的t,设置为鼠标的当前方向:
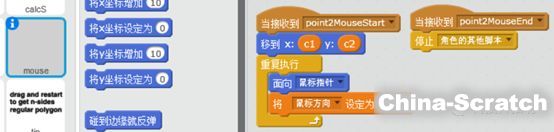
声明:本文章由网友投稿作为教育分享用途,如有侵权原作者可通过邮件及时和我们联系删除